The Solow Growth Model, developed by Nobel Prize-winning economist Robert Solow, is an exogenous model that examines economic output changes over time due to factors like population growth, savings rates, and technological advancements. It is a neoclassical growth model built on the Keynesian Harrod-Domar framework and serves as the foundation for modern economic growth theory. The model assumes a constant population growth rate, with consumers saving a fixed proportion of their incomes and firms utilising the same production technology. It also assumes constant returns to scale, where doubling capital and labour stock results in double the output. The Solow model predicts conditional convergence, suggesting that countries with identical growth rates in population, savings, and capital depreciation will converge economically. However, it does not predict absolute convergence, indicating that countries with different saving rates will have distinct steady states and may not converge. The model also introduces the concept of the Golden Rule savings rate, which maximises steady-state consumption growth by balancing savings and investment for future generations.
| Characteristics | Values |
|---|---|
| Population growth rate | Dictates the steady-state growth rates of all variables in the economy |
| Level variables | Output, Y, consumption, C, capital, K, and labor, L |
| Per capita ratio variables | Output per person, y, capital per person, k, and consumption per person, c |
| Savings rate | A permanent change does not permanently change the economy's growth rate |
| Consumption | Proportional to output |
| Production function | Cobb-Douglas |
| Steady state | The state where the level of capital per worker does not change |
What You'll Learn

The Solow-Swan model and the Golden Rule savings rate
The Solow-Swan model, developed by Robert Solow and Trevor Swan, is a simple yet insightful model used to study long-run economic growth. It is built on the foundation of the Keynesian Harrod-Domar model and is the first neoclassical growth model. The Solow-Swan model introduces the concept of a "steady-state," where the level of capital per worker remains constant over time. This steady-state value, denoted as k*, is influenced by factors such as the savings rate, population growth rate, and capital depreciation rate.
In the Solow-Swan model, agents save a fixed fraction of their current incomes, and these savings are channelled into sustaining or increasing the stock of capital. Capital is then combined with labour to produce output, which is paid out to workers and capital owners. The model assumes a closed economy, implying that domestic investment equals domestic saving.
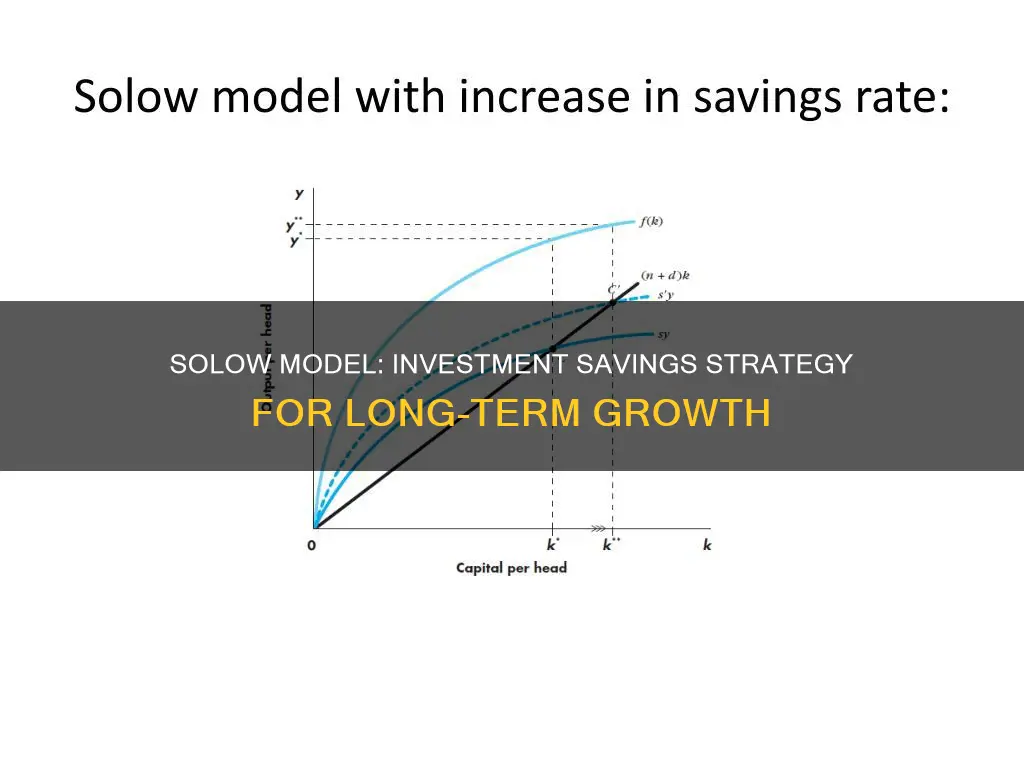
The Solow-Swan model reveals that changes in the savings rate can impact the growth rate of the economy. Increasing the savings rate can lead to a temporary boost in growth rates, but in the long run, growth returns to its previous rate. This phenomenon is known as the Solowian paradox of thrift.
Now, let's introduce the concept of the Golden Rule savings rate. In economics, the Golden Rule savings rate is the rate of savings that maximises the steady-state level of consumption growth. In the context of the Solow-Swan model, this means finding the savings rate that results in the highest possible constant value of per-capita consumption. The Golden Rule savings rate is influenced by factors such as the capital/labour ratio, the population growth rate, and the rate of depreciation of capital.
Mathematically, the Golden Rule savings rate, denoted as s^G, can be expressed as:
> s^G = (n+d)k^G / f(k^G)
Where n is the population growth rate, d is the depreciation rate, and k^G is the golden-rule steady-state level of the capital/labour ratio. The function f(k) represents the resulting per capita output.
The Golden Rule savings rate is important for policymakers as it helps answer the question of whether an economy is saving too much or too little. Various economic policies can be implemented to influence the savings rate and guide it towards the Golden Rule level. For example, consumption taxes can reduce consumption and increase the savings rate, while capital gains taxes can have the opposite effect.
Invest Your Savings Wisely: A California Guide
You may want to see also

The paradox of thrift
According to Keynesian theory, the proper response to an economic recession is more spending, more risk-taking, and less saving. This is because a recessed economy doesn't produce at full capacity, with some factors of production, such as land, labour, and capital, remaining unemployed. Keynesians argue that consumption or spending drives economic growth. While it may be rational for individuals and households to reduce consumption during tough economic times, this can have a detrimental effect on the economy as a whole. A decrease in aggregate consumer spending may force businesses to produce even less, deepening the recession.
Investing Young: Better Than Saving?
You may want to see also

Population growth rate and its implications
The Solow Growth Model, developed by Robert Solow, is an exogenous model of economic growth that analyses changes in the level of output in an economy over time as a result of changes in the population growth rate, savings rate, and rate of technological progress.
The Solow model assumes that the population grows at a constant rate, denoted as 'g'. The current and future populations are linked through the population growth equation: N’ = N(1+g). For example, if the current population is 100 and its growth rate is 2%, the future population will be 102.
The population growth rate has significant implications for the economy. Firstly, it "dictates" the steady-state growth rates of various economic variables, including output, consumption, capital, and labour. In other words, at a steady state, these variables grow at the same natural rate as the population growth rate. As a result, per capita ratio variables, such as output per person, capital per person, and consumption per person, remain constant over time.
Secondly, a change in the population growth rate can impact the rate of economic growth. An increase in the population growth rate leads to a higher growth rate of aggregate output but does not permanently affect the growth rate of per capita output. Instead, an increase in population growth can lower the steady-state level of per capita output.
The Solow model also predicts conditional convergence among countries with the same population growth rate, savings rate, and capital depreciation rate. These countries will converge to the same steady state, and along this path, poorer countries will experience faster growth.
In summary, the population growth rate plays a crucial role in the Solow model, influencing the growth rates of economic variables, the level of output, and the convergence of countries. Understanding the implications of population growth is essential for economic analysis and policy-making within the framework of the Solow model.
Maximizing HSA Savings: Investment Strategies for Tax-Free Growth
You may want to see also

Savings rate and consumption
The Solow Growth Model, developed by Robert Solow, is an exogenous model of economic growth that analyses changes in the level of output in an economy over time as a result of changes in the population growth rate, the savings rate, and the rate of technological progress. It assumes that all consumers in the economy save a constant proportion, 's', of their incomes and consume the rest. Therefore, consumption (represented by C) and output (represented by Y) are linked through the consumption equation C = (1-s)Y. For example, if a consumer earns 100 units of output as income and the savings rate is 40%, they will consume 60 units and save 40 units.
The Solow model predicts that a permanent change in the rate of savings, s, will not permanently change the economy's growth rate. For instance, an increase in the savings rate will initially increase the growth rate of capital, output, and consumption. However, as the new steady-state ratio is approached, the growth rate of capital, output, and consumption will slow down and eventually return to the previous growth rate. This is known as the Solowian paradox of thrift.
The Solow model also implies that the steady-state growth is, in general, consumption inefficient. This means that the economy's steady state does not yield the highest consumption per capita. For example, if the savings propensity is high, the steady-state per capita consumption may be lower than what could be potentially achieved. In such cases, decreasing the savings rate could increase per capita consumption permanently.
The Golden Rule savings rate is the rate of savings that maximises the steady-state level of consumption growth. It aims to achieve the highest possible constant value of per-capita consumption. The Golden Rule savings rate is influenced by factors such as the population growth rate, the rate of depreciation of capital, and the production function. Economic policies, such as consumption taxes and capital gains taxes, can also impact the savings rate and help achieve the Golden Rule level of savings.
In summary, the Solow Growth Model highlights the relationship between savings, consumption, and economic growth. While increasing the savings rate may lead to temporary growth acceleration, it will not have a permanent effect on growth rates. The model suggests that finding the optimal savings rate, such as the Golden Rule savings rate, can help maximise consumption efficiency and achieve the highest possible steady-state consumption per capita.
Savings or Investing: Where Should Your Money Go?
You may want to see also

Capital depreciation and investment
The Solow Growth Model, developed by Nobel Prize-winning economist Robert Solow, is an exogenous model of economic growth that examines changes in output levels in an economy over time. It is founded on three main components: technology, capital accumulation, and savings.
The model's capital accumulation equation explains how capital stock evolves in an economy. Capital accumulation is influenced by the rate of physical depreciation and investment. The amount of capital per capita at the start of a period, denoted as kt, is impacted by depreciation, represented by δ, which reduces the capital stock over time. Simultaneously, investment, denoted as it, adds new capital for the subsequent period. The capital accumulation equation is expressed as:
Kt+1 = kt(1 − δ) + it
Or alternatively, as:
Kt+1 = kt(1 − δ) + sAf(kt)
Where s represents savings, A represents technology, and f(kt) signifies the per capita production function.
The Solow model assumes a constant rate of capital depreciation, denoted as d, and considers it as an exogenous variable. This rate influences the evolution of capital stock over time, as reflected in the capital accumulation equation.
The Solow Growth Model predicts that in the long term, there is no growth. This prediction is based on the assumption that countries with identical population growth rates (g), savings rates (s), and capital depreciation rates (d) will converge to the same steady state. However, countries with differing savings rates will not converge, indicating that lower initial capital stock does not always equate to higher growth.
The model also introduces the concept of the steady state, where the level of capital per worker remains unchanged. This steady state, denoted as k*, is determined by the equation:
K* = k*(1 − δ) + sAf(k*)
At this point, the amount of capital lost due to depreciation is counterbalanced by savings, resulting in a net investment of zero. The economy exhibits stability, tending towards the per capita capital stock k*.
Smart Ways to Invest Your RBFCU Savings
You may want to see also
Frequently asked questions
The Solow Growth Model is an exogenous model of economic growth that analyses changes in the level of output in an economy over time as a result of changes in the population growth rate, the savings rate, and the rate of technological progress.
There is no growth in the long term. If countries have the same population growth rate, savings rate, and capital depreciation rate, then they will have the same steady state and will converge. Along this convergence path, a poorer country grows faster.
The Golden Rule savings rate is the rate of savings that maximises the steady-state level of consumption growth. In the Solow-Swan model, this implies that all income is going towards investment capital for future production.
The Solowian paradox of thrift claims that a permanent change in the rate of savings will not permanently change the economy's growth rate. For example, an increase in the savings rate will only increase growth rates temporarily and, in the long run, will have no effect.