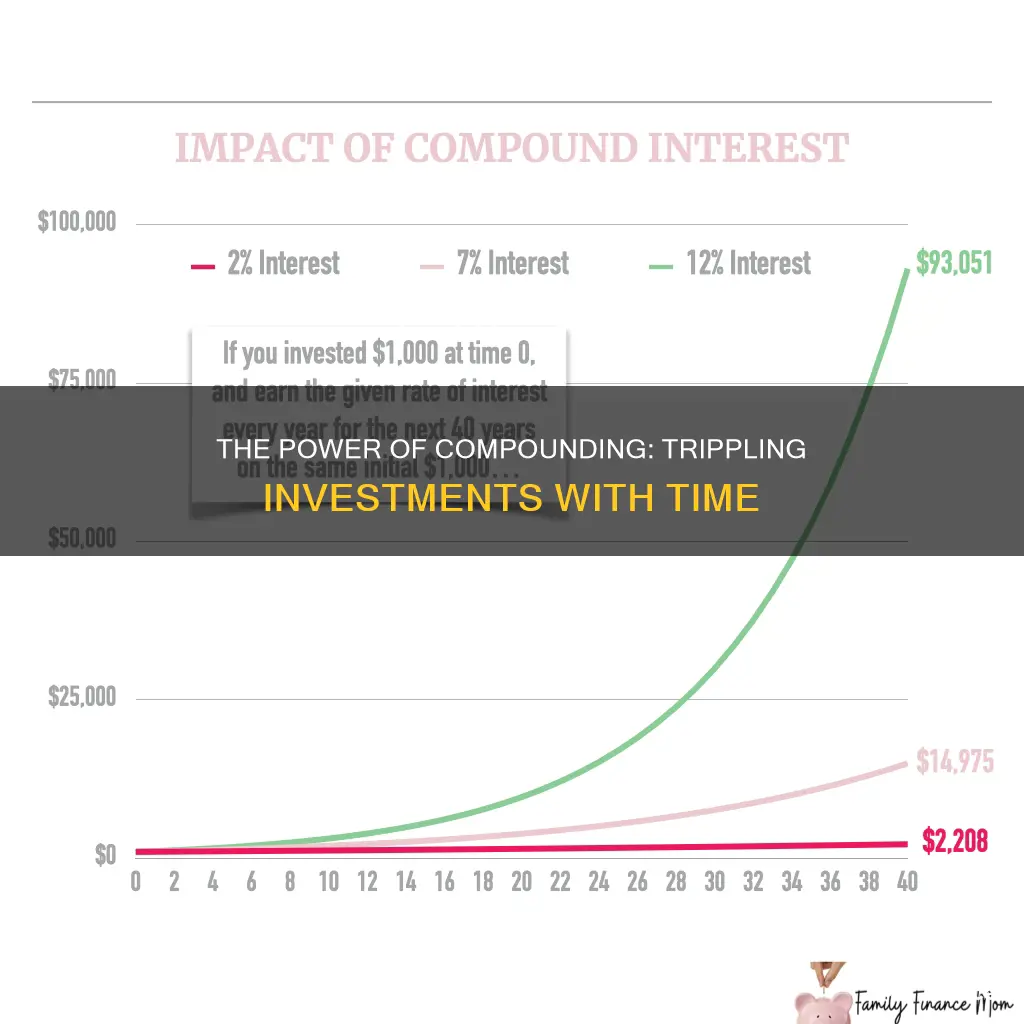
The amount of time it takes for an investment to triple depends on the interest rate. For example, if an investment has a continuous interest rate of 5%, it will take around 22 years to triple. If an investment has an interest rate of 7% and the interest is compounded annually, it will take around 16.4 years to triple.
| Characteristics | Values |
|---|---|
| Time taken for an investment to triple at 5% interest | ~22 years |
| Time taken for an investment to triple at 7% interest | 16.4 years |
What You'll Learn

How long to triple an investment with 5% compound interest
If you are earning compound interest at a rate of 5%, it will take approximately 22 years for your investment to triple. This is calculated using the compound interest formula: A = Pert.
Where A is the current value, P is the initial investment, r is the rate, and t is time. If an investment triples, that means A is currently equal to 3*P.
The rules of 72 and 115 provide a quick way of seeing the value and speed of compounding. These are shortcuts to determine how long it takes compounded money to double and triple. To calculate how long it takes money to triple, divide the interest rate into 115.
Diverse Investments: Do They Dilute Interest Earnings?
You may want to see also

Rules of 72 and 115
The rules of 72 and 115 are shortcuts to determine how long it takes for an investment to double and triple. To calculate how long it takes money to double, divide the interest rate into 72. To see how long money triples, divide it into 115. For example, assuming a 7% interest rate, it will take approximately 10.3 years for the original principal to double and 16.4 years to triple.
The rules of 72 and 115 are useful for quickly estimating the value and speed of compounding. Compounding can be daily, monthly, annually or any other way that a lender and borrower agree. Effective annual yield quotes take compounding into account over the investment period or term.
The formula for calculating compound interest is: A = Pert, where A is the current value, P is the initial investment, r is the rate, and t is time. If an investment triples, that means A is currently equal to 3*P. For example, if an investment has an interest rate of 5% (or 0.05), the formula would be: 3P = Pe0.05*t.
Using the rule of 115, if an investment has an interest rate of 5%, it will take approximately 22 years for the investment to triple.
Interest Rates: The Investment Influencer
You may want to see also

How to calculate the value and speed of compounding
The rules of 72 and 115 provide a quick way of seeing the value and speed of compounding. These are shortcuts to determine how long it takes compounded money to double and triple. To calculate how long it takes money to double, divide the interest rate into 72. To see how long money triples, divide it into 115. For example, assuming a 7% interest rate, it will take approximately 10.3 years for the original principal to double and 16.4 years to triple.
The compound interest formula is: A = Pert, where A is the current value, P is the initial investment, r is the rate, and t is time. If an investment triples, that means A is currently equal to 3*P. For example, if the interest rate is 5% (or 0.05), the formula would be: 3P = Pe0.05*t, or 3 = e0.05t, or ln(3) = 0.05*t, or t = ln(3)/0.05. This means it would take around 22 years for the investment to triple.
Negative Interest Rates: Incentivizing Firms to Invest?
You may want to see also

The compound interest formula
If an investment triples, this means that A is currently equal to 3*P. For example, if you invest £100 at a rate of 5% interest, your investment will be worth 3*£100 = £300 when it has tripled.
To calculate how long this will take, you can use the formula: 3P = Pe^rt. This can be rearranged to give: t = ln(3)/r. So, for an investment of £100 at 5% interest, it will take approximately 22 years to triple in value.
The rules of 72 and 115 provide a quick way of seeing the value and speed of compounding. To calculate how long it takes money to triple, divide the interest rate into 115. For example, at an interest rate of 7%, it will take approximately 16.4 years for an investment to triple.
Understanding Investment Interest Charges: Strategies for Success
You may want to see also

How to calculate the time it takes for an investment to triple
To calculate the time it takes for an investment to triple, you can use the compound interest formula: A = Pert. In this formula, A is the current value, P is the initial investment, r is the rate, and t is time. If an investment triples, A is currently equal to 3*P.
For example, if you have an interest rate of 5% (or 0.05), you can calculate the time it takes for an investment to triple using the following steps:
- 3P = Pe^0.05*t
- 3 = e^0.05t
- Ln(3) = 0.05*t
- T = ln(3)/0.05
- T = ~22 years
Alternatively, you can use the rule of 115 to determine how long it takes for an investment to triple. This rule is a shortcut that allows you to quickly estimate the time it takes for compounded money to triple. To use this rule, simply divide the interest rate into 115. For example, with a 7% interest rate, it will take approximately 16.4 years for the original principal to triple.
Understanding Interest: Investment Strategies Simplified
You may want to see also
Frequently asked questions
It will take approximately 22 years for an investment to triple if interest is compounded continuously at 5%.
It will take approximately 16.4 years for an investment to triple if interest is compounded annually at 7%.
The rule of 115 provides a quick way of seeing the speed of compounding. To calculate how long it will take for an investment to triple, divide the interest rate into 115.