The formula for calculating how long it takes for an investment to triple in value involves the principal amount, the rate of interest, and the number of years. Using this formula, you can determine the time it will take for your investment to reach three times its original value. For example, if you invest at a rate of 5% compounded annually, it will take approximately 22.52 years to triple your investment. Similarly, at a rate of 6% compounded annually, your investment will triple in 10 months.
| Characteristics | Values |
|---|---|
| Formula | A = accumulated amount, P = initial investment, r = rate, and t = time |
| Variables | p = principal investment, r = interest rate, n = # times compounded per year |
| Calculation | log(3) = t log(1 + r/n) Divide by log(1 + r/n) on both sides of the equation t = log(3) / log(1 + r/n) |
| Example 1 | 5% interest compounded annually: t = 22.52 years |
| Example 2 | 3% compounded monthly: t = 36 years 8 months |
What You'll Learn

Calculating compound interest
To calculate compound interest, you'll need to know the compound interest formula: A=P(1+r/n)^nt.
- A = ending amount
- P = original balance
- R = interest rate (as a decimal)
- N = number of times interest is compounded in a specific time frame
- T = time frame
For example, if you deposit $5,000 in a savings account that earns a 5% annual interest rate and compounds monthly, you would calculate A = $5,000(1 + 0.00416667/12)^(12 x 1), and your ending balance after one year would be $5,255.81.
You can also use an online compound interest calculator to work out the accrued amount, principal amount, rate of interest, or time.
For example, if you have an investment account that increased from $30,000 to $33,000 over 30 months, and you want to know what annual interest rate you need to get to match the rate of return in your investment account, you can use the formula r = n((A/P)1/nt - 1). In this case, the answer is 3.813% per year.
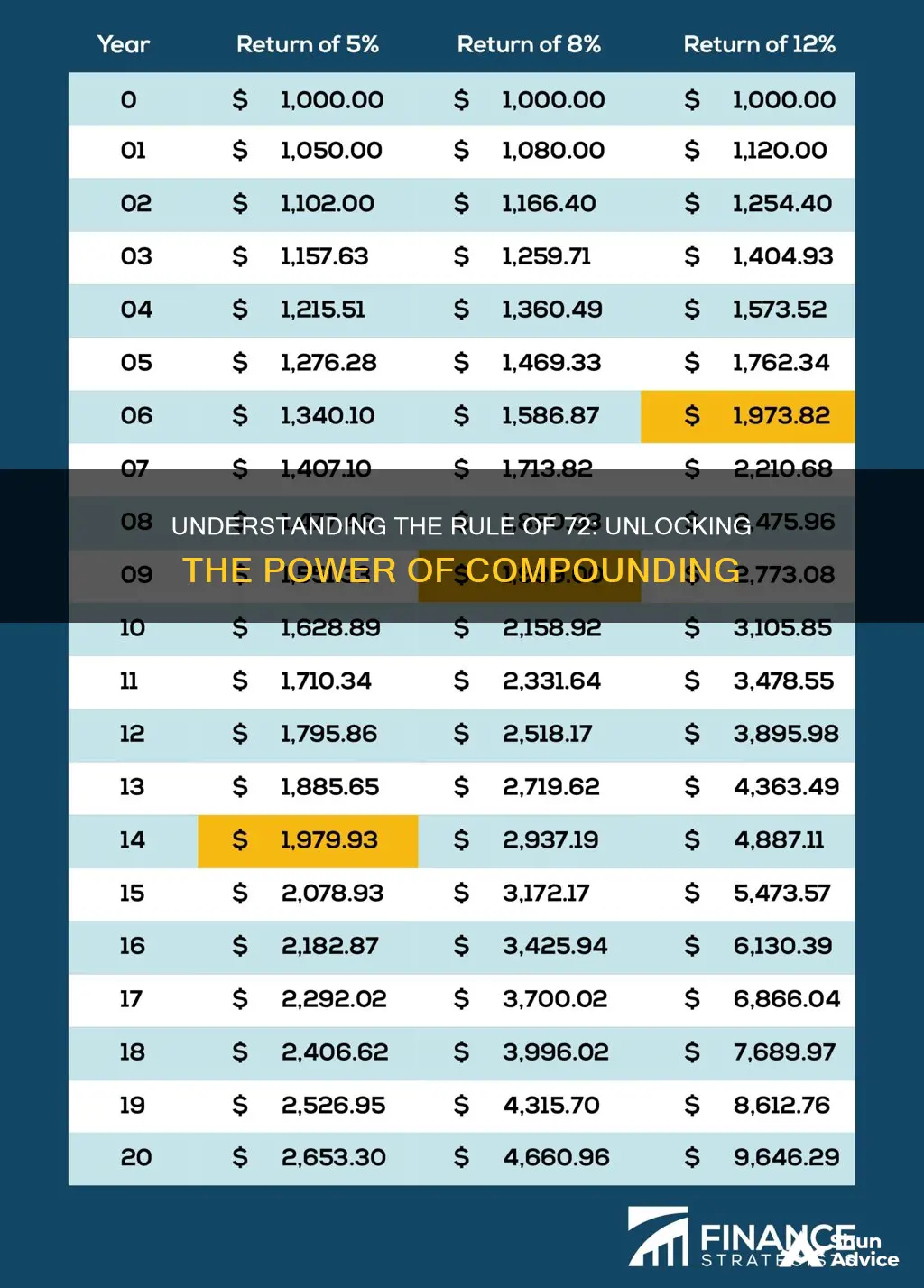
Compound interest is a powerful tool for growing your savings over time. For example, if you put $10,000 into a high-yield savings account with a 5% annual yield, compounded daily, you will earn $512.67 in interest in the first year. If you leave your money in the account for another year, you'll earn $538.96 in interest in year two, for a total of $1,051.63 in interest over two years. After 10 years, you will have earned $6,486.65 in interest for a total balance of $16,486.65.
Tuscan Gardens Retirement: A Sound Investment Strategy?
You may want to see also

Variables: A, P, r, t
To determine how long it will take for an investment to triple, we can use the compound interest formula, where:
- A = accumulated amount
- P = principal investment
- R = interest rate in decimal form
- N = number of times compounded per year
- T = time
If an investment triples, the current value (A) is equal to 3*P (the initial investment multiplied by 3).
To find the time (t) it will take for an investment to triple at a given interest rate (r), you can set up and solve an equation using the above formula. For example, if the interest rate is 5% (or 0.05 as a decimal) compounded annually (n=1), the equation would be as follows:
3P = P(1+r)^t
Taking the logarithm of both sides, we get:
Log(3) = tlog(1+r)
Dividing both sides by log(1+r), we find:
T = log(3)/log(1+r)
Plugging in the value for r (0.05), we can calculate the time it will take for the investment to triple:
T = log(3)/log(1.05)
Using a calculator, we find that t is approximately 22.52 years.
So, it will take approximately 22.52 years for the investment to triple at a 5% annual interest rate.
The same formula can be used for different interest rates and compounding periods. For example, if the interest rate is 3% compounded monthly (n=12), the equation becomes:
3P = P(1+0.03/12)^12t
Following similar steps as before, we can solve for t to find the time it takes for the investment to triple.
Rich Investors: Why Startups?
You may want to see also

Logarithms
To answer your first question, "how long will it take an investment to triple" depends on the interest rate and the number of compounding periods per year.
Now, for logarithms:
History of Logarithms
Logarithm Types and Uses
The logarithm base 10 is called the decimal or common logarithm and is used in science and engineering. The natural logarithm has the number e (approximately 2.718) as its base and is used in mathematics and physics. The binary logarithm uses base 2 and is common in computer science.
Logarithmic scales are useful for reducing wide-ranging quantities to smaller, more manageable scopes. For example, the decibel (dB) is a unit expressing ratios as logarithms, often used for signal power and amplitude. Logarithms are also used in chemistry to measure the acidity of an aqueous solution; the pH is a logarithmic measure.
Logarithm Derivatives and Antiderivatives
As the exponential function is the inverse of the logarithmic function, the properties of the exponential function allow us to derive the derivative and antiderivative of the logarithmic function. The derivative of logb x is given by 1/(x*ln(b)). The antiderivative of the natural logarithm ln(x) is x*ln(x) - x + C.
Wyndham's Annual Investor Count
You may want to see also

Annual interest rates
The formula for continuously compounded interest is:
A = Pe^(rt)
Where:
- A is the final amount
- P is the principal amount or starting point
- R is the rate of growth (as a decimal)
- T is the time
If you want to work out how long it will take for your investment to triple, you can rearrange the formula to solve for t:
- A = 3P (as the final amount is three times the principal amount)
- Substitute A = 3P into the formula: 3P = Pe^(rt)
- Divide both sides by P: 3 = e^(rt)
- Take the natural logarithm (ln) of both sides: ln(3) = rt
- Divide both sides by r: t = ln(3)/r
- Plug in your rate of interest (as a decimal) to calculate t, the time it will take for your investment to triple.
For example, if you have an annual interest rate of 5.3%, you would calculate this as follows:
- T = ln(3)/0.053
- T = 20.728 or 21 years
Alternatively, you can use the Rule of 72 to estimate how long it will take for your investment to double. This is a simplified version of the compound interest calculation. Divide 72 by the interest rate to estimate how long it will take to double your money. For example, if your interest rate is 6%, it will take 12 years to double your money (72/6 = 12).
Retirement Planning: Navigating the Impact of Diverse Investment Choices
You may want to see also

Monthly vs. annual compounding
The number of times an investment is compounded over a given period will affect the total interest accrued. Compounding interest is a key concept in understanding wealth-building. The shorter the compounding period, the higher the effective yield.
Compounding interest more than once a year is called intra-year compounding. Interest may be compounded semi-annually, quarterly, monthly, daily, or even continuously. When interest is compounded more than once a year, this affects both future and present-value calculations.
With intra-year compounding, the periodic interest rate, instead of being the stated annual rate, becomes the stated annual rate divided by the number of compounding periods per year. The number of periods, instead of being the number of years, becomes the number of compounding periods per year multiplied by the number of years.
For example, with monthly compounding, the stated annual interest rate is divided by 12 to find the periodic (monthly) rate, and the number of years is multiplied by 12 to determine the number of (monthly) periods.
Let's say you have a balance of $100,000 in a savings account that pays interest of 3% per year. If you withdraw your $3,000 interest at the end of the first year, your remaining principal will be $100,000, the amount with which you started. Your interest the second year at 3% will again be $3,000. This is an example of simple interest.
If you leave the interest in the savings account at the end of the first year, its balance at the end of the year will be $103,000. Because the balance in your account has increased, the interest at 3% for the second year will also grow, in this case to $3,090, and therefore your total balance at the end of the second year will be $106,090.
You can see that the longer you leave your money in your savings account, the higher your interest will be every year because you'll be earning interest on the interest earned in previous years. This phenomenon, where you earn interest on interest, is called compound interest.
Now, let's compare annual and monthly compounding. If you see a bank advertising that they compound interest monthly, it means that, instead of waiting until the end of the year to calculate interest and add it to your account, they do it at the end of every month. So, at the end of the first month, your interest would be $250, or 1/12th of the $3,000 annual interest. After they add the interest of $250 to your balance, the principal at the end of January will become $100,250. You can see the interest for February will be slightly higher, $250.625 to be exact. Interest for every succeeding month will also grow correspondingly. March's will be $251.25, and so on.
At the end of the year, your total interest will come to $3,041.60 if your bank compounds interest monthly. That's $41.60 higher than the $3,000 compared to the earlier example of annual compounding.
The difference between annual and monthly compounding is not that big, though, and likewise, the difference between daily and monthly compounding will also be minor. The principle carries through: the shorter the interval used for compounding, the higher your interest earned will be.
The Wealthy Retiree's Investment Playbook: Strategies for Preserving and Growing Your Nest Egg
You may want to see also
Frequently asked questions
The formula is: log(3) = t log(1+interest rate as a decimal).
It will take 22.52 years to triple the investment.
It will take 10 months to triple the money.