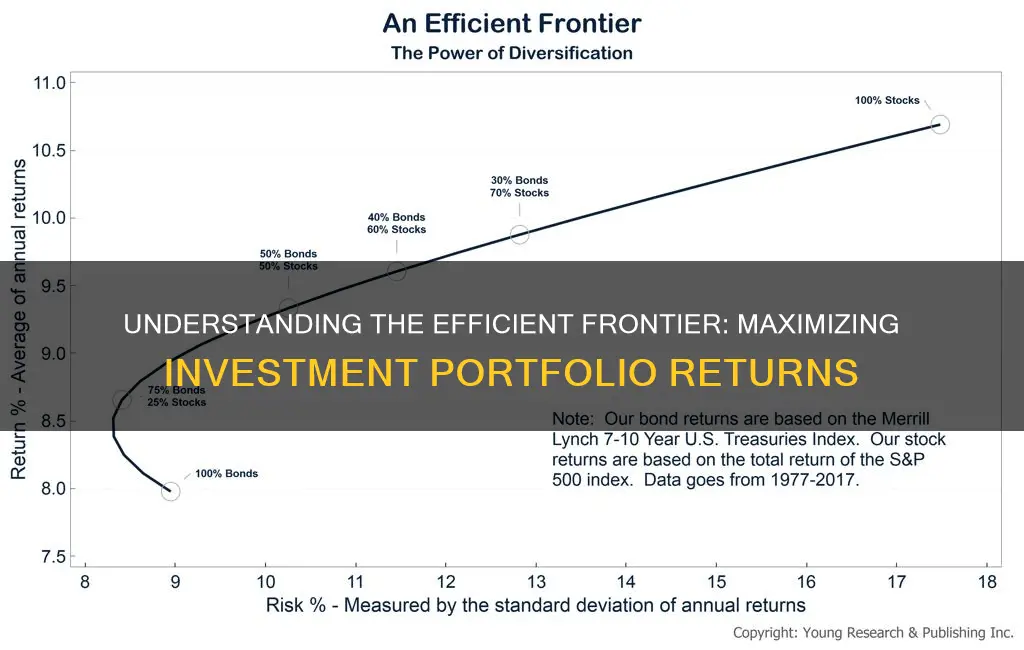
The efficient frontier is a cornerstone of modern portfolio theory, and was first introduced by Harry Markowitz in 1952. It is a set of investment portfolios that are expected to provide the highest returns for a given level of risk. The efficient frontier is curved because every increase in risk results in a smaller amount of returns. Portfolios that fall below the efficient frontier are sub-optimal because they do not provide enough return for the level of risk. The efficient frontier is important because it helps investors understand the potential risks and returns in their portfolios and change their investing strategies accordingly.
| Characteristics | Values |
|---|---|
| Definition | A set of optimal investment portfolios that offer the highest expected return for a defined level of risk. |
| Graphical Representation | The efficient frontier is a curved line. It is concave to the Y-axis. |
| Axes | The expected return is plotted on the y-axis, and the standard deviation as a measure of risk is plotted on the x-axis. |
| Diversification | Diversifying assets in a portfolio leads to increased returns and decreased risks, resulting in a portfolio located on the efficient frontier. |
| Investor Risk Tolerance | The efficient frontier depends on the investor's degree of risk tolerance. Risk-seeking investors would select investments on the right end of the frontier, while conservative investors would choose investments on the left side. |
| Applicability | The efficient frontier is not a one-size-fits-all concept. It is tailored to each investor's specific requirements and factors such as the number of assets, industry, and risk tolerance. |
| Limitations | The efficient frontier is based on assumptions that may not reflect reality, such as rational investors, unlimited access to borrowing, and normal distribution of asset returns. |
What You'll Learn

Efficient Frontier as a foundation for modern portfolio theory
The efficient frontier is a cornerstone of modern portfolio theory (MPT). Introduced by Harry Markowitz in 1952, it won him the Nobel Prize in 1990.
The efficient frontier is a set of optimal portfolios that offer the highest expected return for a defined level of risk. It is a foundation for modern portfolio theory because it helps investors understand the potential risks and returns in their portfolios and how they compare to the optimal set of portfolios. This knowledge allows investors to change their strategies according to the level of risk they are willing to take.
The efficient frontier is represented by plotting the expected returns of a portfolio against the standard deviation of returns, which is a measure of risk. The y-axis is made up of the expected returns of the portfolio, and the x-axis is the standard deviation of returns. A portfolio is then plotted onto the graph according to its expected returns and standard deviation of returns. The portfolio is then compared to the efficient frontier. If a portfolio is plotted on the right side of the chart, it indicates a higher level of risk, and if it is plotted low on the graph, it offers lower returns.
The efficient frontier is curved because every increase in risk results in a relatively smaller amount of returns. This is known as the diminishing marginal return to risk. The curvature of the efficient frontier also visually demonstrates the benefits of diversification and how it can improve a portfolio's risk versus reward profile.
It is important to note that the efficient frontier is built on assumptions that may not always reflect reality. For example, it assumes that investors are rational and avoid risk when possible, that there are not enough investors to influence market prices, and that all investors have unlimited access to borrowing and lending money at a risk-free interest rate.
Rajiv Gandhi Equity Savings Scheme: A Smart Investment Move
You may want to see also

How to plot Efficient Frontier on a graph
The efficient frontier is a cornerstone of modern portfolio theory (MPT) and was introduced by Harry Markowitz in 1952. It is a graph that rates portfolios on a scale of return (y-axis) versus risk (x-axis).
To plot the efficient frontier on a graph, you will need to follow these steps:
Firstly, determine the expected return and risk of each individual investment in your portfolio. The expected return is the weighted average of the expected returns of the individual investments, while the risk is typically measured by the standard deviation of returns.
Next, combine these investments in different proportions to create multiple portfolios with varying risk-return profiles. You can do this by assigning different weights to each investment within the portfolio. This step will allow you to calculate the expected return and risk for each portfolio combination.
Now, you can plot these portfolios on an XY scatter graph, with risk on the x-axis and return on the y-axis. This scatter graph will represent the efficient frontier, showing all feasible portfolio combinations.
Additionally, you can include a minimum variance portfolio (MVP) on the graph, which represents the minimum risk an investor would accept. The efficient frontier will curve backward, indicating the benefits of diversification due to negative correlation.
Finally, you can also plot an investor's utility function, based on their level of risk aversion, on the same graph. The point of intersection between the efficient frontier and the utility curve will represent the optimal portfolio allocation given the investor's risk-return trade-off and risk aversion.
By plotting the efficient frontier, you can visually identify efficient portfolios that offer the highest return for a defined level of risk or the lowest risk for a given level of expected return.
Mastering Your Investment Portfolio with Excel
You may want to see also

The importance of diversification
The efficient frontier is a cornerstone of modern portfolio theory, and diversification is a key component of this theory. The efficient frontier comprises investment portfolios that offer the highest expected return for a specific level of risk. It is important to understand the role of diversification in achieving this optimal balance between risk and return.
Diversification is the process of spreading investments across different asset classes, industries, sectors, companies, and geographic regions. The main goal of diversification is to reduce the overall risk of an investment portfolio. By holding a variety of investments, the poor performance of one investment can potentially be offset by the better performance of another, leading to a more consistent overall return. Diversification aims to include assets that are not highly correlated with one another, as this helps to lower the portfolio's standard deviation and overall risk.
Most investment professionals agree that diversification is crucial for reaching long-term financial goals while minimising risk. It is important to note that diversification does not guarantee against losses, but it helps to manage and mitigate risk. Unsystematic or diversifiable risk can be significantly reduced through diversification, while systematic or market risk is generally unavoidable.
The benefits of diversification include increased risk-adjusted returns, preservation of capital (especially for retirees or older investors), and the creation of better investment opportunities. Additionally, diversification can make investing more enjoyable, as it involves researching new industries and comparing companies.
However, there are also potential drawbacks to diversification. Managing a diverse portfolio can be cumbersome and complicated, especially with multiple holdings and investments. Diversification can also be expensive due to transaction fees and brokerage charges. It is important to strike a balance between diversification and maximising returns, taking into account risk tolerance and investment goals.
Saving and Investment Macroeconomics: The Basics of Money Management
You may want to see also

The limitations of the Efficient Frontier theory
The efficient frontier theory, introduced by Harry Markowitz in 1952, is a cornerstone of modern portfolio theory. It rates portfolios on a scale of return (y-axis) versus risk (x-axis). The efficient frontier comprises investment portfolios that offer the highest expected return for a specific level of risk.
However, the efficient frontier theory has its limitations. Here are some of the key limitations:
- Assumptions of Normal Distribution: The theory assumes that asset returns follow a normal distribution. However, in reality, securities may experience returns (tail risks) that deviate significantly from the mean, following a leptokurtic or heavy-tailed distribution. This assumption may not accurately represent the true nature of asset returns.
- Rational Investors: Markowitz's theory assumes that investors are rational and avoid risk when possible. However, in practice, the market includes irrational and risk-seeking investors whose behaviours can significantly impact prices and market trends.
- Market Influence: The theory assumes that there are not enough investors to influence market prices. Nevertheless, large market participants, such as institutional investors or high-net-worth individuals, can sway prices and disrupt the equilibrium assumed by the efficient frontier theory.
- Access to Capital: The efficient frontier theory assumes that investors have unlimited access to borrowing and lending money at the risk-free interest rate. In reality, access to capital varies across investors, and borrowing costs can significantly impact investment strategies and portfolio construction.
- Model Instability: Academics have found that the efficient frontier model can be unstable, particularly when reference assets have a high degree of correlation. This instability can affect the reliability of the model's outputs and recommendations.
- Diversification Challenges: While the efficient frontier theory emphasises the benefits of diversification, it may be challenging to achieve optimal diversification in practice due to various factors such as transaction costs, liquidity constraints, or regulatory limitations.
These limitations highlight the gap between theoretical assumptions and real-world complexities in investment portfolios. While the efficient frontier provides a valuable framework for analysing and constructing portfolios, it is essential to recognise these limitations and consider them when applying the theory in practical investment decision-making.
Saving or Investing: Where Should Your Money Go?
You may want to see also

How to use Efficient Frontier to select investments
The efficient frontier is a concept in finance that can help you identify a potential portfolio for any given return requirement and level of risk. The concept was developed in 1952 by Harry Markowitz and has since been used to help investors build portfolios with higher expected returns and lower associated risks.
The efficient frontier comprises investment portfolios that offer the highest expected return for a specific level of risk. It represents, in graphical form, portfolios that maximise returns for the risk assumed, showing the benefit of diversification.
To use the efficient frontier when selecting investments, a risk-seeking investor would choose investments that fall on the right side of the frontier. These securities are expected to have a high degree of risk coupled with high potential returns, which is suitable for highly risk-tolerant investors. Conversely, a more conservative investor would pick investments that lie on the left side of the frontier. These securities are expected to have a lower degree of risk coupled with lower potential returns, which is suitable for risk-averse investors.
The efficient frontier can be used to make more informed real estate investing decisions. It helps investors analyse the potential returns and risks of an investment portfolio, allowing them to better adjust their individual investments or reallocate their assets accordingly to help manage significant financial losses.
The efficient frontier can be calculated using the following formula:
E(Rp) = w1E(R1) + w2E(R2)
Where "w" represents the weight of each asset, and all assets must add up to 1. The "E(R)" is the expected return of every asset in the portfolio.
Retirement Planning: Understanding 401(k) Investment and Savings Plans
You may want to see also
Frequently asked questions
The efficient frontier is a set of optimal investment portfolios that offer the highest expected return for a defined level of risk.
An optimal portfolio is one that is designed with a perfect balance of risk and return. It aims to balance securities with the greatest potential returns with an acceptable degree of risk.
The efficient frontier theory was introduced by Nobel Laureate Harry Markowitz in 1952. It rates portfolios on a scale of return (y-axis) versus risk (x-axis). The efficient frontier graphically represents portfolios that maximise returns for the risk assumed.
The efficient frontier is constructed by plotting the expected returns of a portfolio against the standard deviation of returns. The y-axis represents the expected returns, while the x-axis represents the standard deviation of returns, which is a measure of risk.







